来源:WSDM ’19
研究背景
目标领域
对于终端用户(end user)来说,知识图谱(KG)的结构往往过于复杂,难以访问有价值的信息,基于知识图的问答(QA-KG)旨在解决这一问题,以让用户更高效的获取知识图谱中蕴含的讯息。举例说明:
Q:Which Olympic was in Beijing?
QA-KG旨在确定这个问题相关的两个事实,用三元组的形式可以表示为
(Beijing,Olympics_participated_in,2008 Summer Olympics)
挑战
谓语在自然语言中存在多种不同的表达方式。
例:谓语person.nationality可以表示为
- “what is … ’s nationality”
- “which country is … from”
- “where is … from”
三种形式。
模糊或者不全的实体名会导致答案的数量过于庞大。
例:”How old is Obama?”
只包含了Barak Obama这一实体的一部分。
用户提出问题的领域五花八门,没有哪一个知识图谱能够涵盖所有领域。
改进
- 提出了一种以知识图谱嵌入为基础的问答系统框架(KEQA),将问题中的头部实体,谓语,尾部实体嵌入到向量空间,用以解决上述的三个问题。
- 提出了一种考虑知识图谱中结构和关系差异的联合距离度量方式。
KEQA
为什么使用KGE(知识图谱嵌入)技术?
知识图嵌入目标用于学习KG中每个谓词/实体的低维矢量表示,使得原始关系在矢量中得到很好的保留。 这些学习的矢量表示可用于有效地完成各种下游应用。目前已经有了知识图谱补全、关系提取、推荐系统等方面的应用。
KEQA的主要思想

如图所示,图谱G被嵌入到了两个低维的向量空间中,包括谓语嵌入空间和实体嵌入空间。每个事实三元组$(h,l,t)$都有其向量表示$(e_h,p_l,e_t)$。给定一个问题Q,首先要学习到该问题的$e_h$、$p_l$,并且预测出$e_t$,组成“预测事实”,再通过度量向量距离寻找同预测事实最接近的事实,就能得到该问题可能的答案。
知识图谱的嵌入
文章简单描述了所采用的嵌入方法,其核心思想与TransE、TransR相同,都是通过最小化$e_t$和$f(e_h,p_l)$之间的距离来得到实体和关系的嵌入(函数$f(·)$是用来衡量三元组中向量关系的函数。TransE中$f(e_h,p_l)=e_h+p_l$),文章没有明确具体是哪一种方法。
谓语和头部实体学习模型
给定一个简单问题,目标是找到谓语向量空间中的一点来作为该问题的谓语向量$p_l$,在实体向量空间中找到一点作为头部实体向量$e_h$。该模型的核心思想是考虑不同问题中词的语序(order)和词的重要性(importance),为此文中引入了双向LSTM和注意力机制。关于词的重要性,文章中举例说明:当我们在学习谓语的向量时,实体就显得不那么重要了。
谓语表示学习
谓语,只得是一句话中用来描述主语的部分,如John went home中的went home。
一般预测谓语的方法包括:
- 学习基于语义解析的映射,再人为的标注语义;
- 为每个谓语做标注,转化成分类任务
文章提出,用户提出问题的领域会非常广泛,以至于一个新问题的谓语可能与其他所有已有的谓语都不相同。
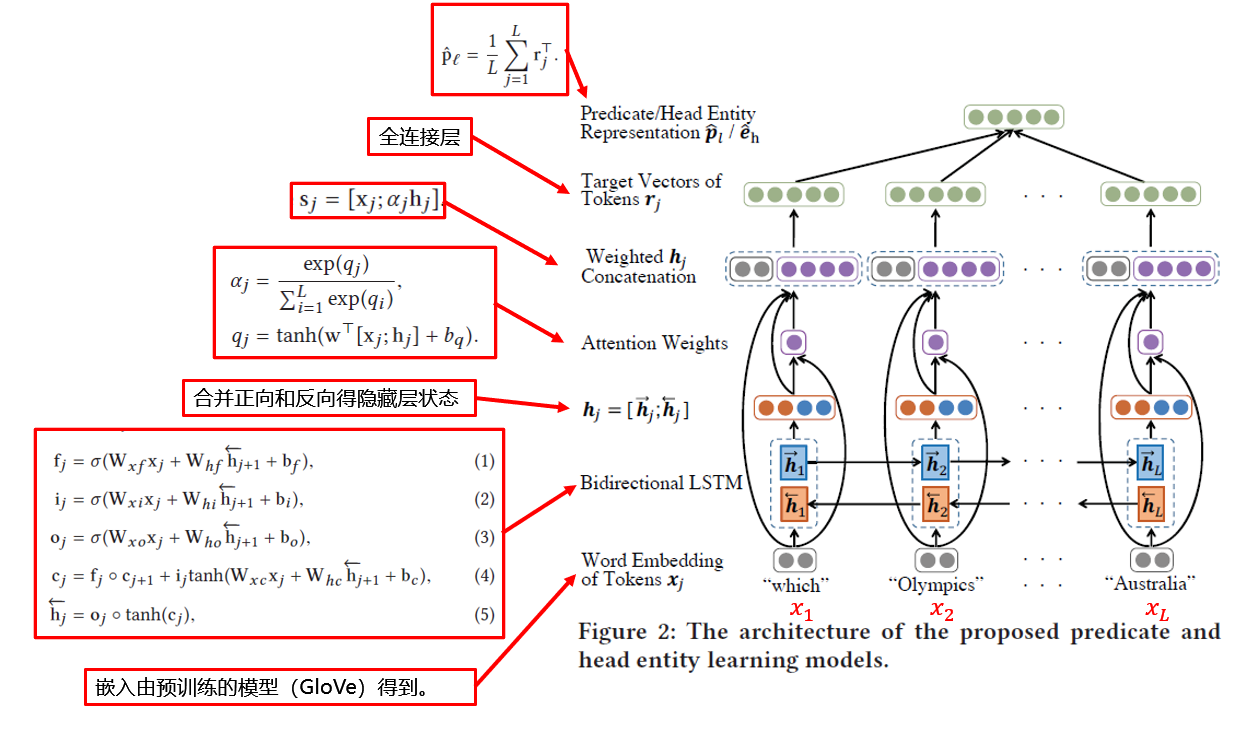
模型训练时的目标是:输入一个已知答案的简单问句,找到离$p_l$(标注)最近的$\hat p_l$(预测)
头部实体表示学习及头部实体识别
神经网络的结构与谓语表示学习相同,不同点在于图谱中的实体数往往非常庞大,如果要将$\hat e_h$与每一个实体的$e_h$比较的话耗费会非常大,因此文章引入了一个头部实体检测模型HED,该模型的训练集是一系列已知事实的问题,其结构如图所示:
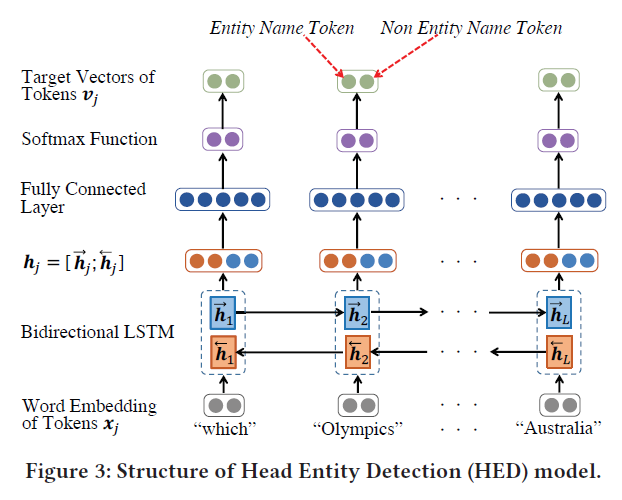
可以观察到该网络与谓语表示学习网络的结构也十分相似,不同点在于没有Attention,同时输出结果$v_j$是一个二维的向量,其含义如图。很明显,该模型的训练目标是找到与已知事实中的头部实体名称相同的token。
利用训练过的HED模型,我们可以标记出问题中的实体名称,所有包含该实体名称的实体都将作为候选实体。
简单来说,这一步在做实体名称的模糊匹配,比如问题是“How old is Obama?”,HED识别出了实体名称”Obama”,包含该实体名称的实体包括”Barak Obama”,”Michelle Obama”,”Obama”等等,这些实体所属的三元组都将被列为候选三元组,相比之下,查找范围缩小了很多,也在一定程度上解决了实体名称不全的问题。但该方法仍有不足,因为KG会有很多实体是同名的。
向量空间上的联合搜索
前面的部分能够得到一个问题谓语和头部实体的表示$\hat p_l和\hat e_h$,以及若干个候选三元组,最后的任务是在候选三元组中找到最符合条件(距离最近)的三元组,距离的计算公式如下:
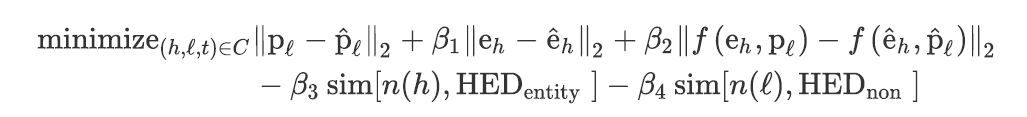
第一行表示候选三元组与预测结果在空间上的距离,其中尾部三元组的向量表示$e_t$由$f(e_h,p_t)$求得,而不是直接选用候选三元组中的$e_t$,这样做是因为在图谱中可能会存在$e_h,p_l$相同但$e_t$不同的情况;
第四项表示尽量选择候选实体名称与标记出的$HED_{entity}$相同的三元组;
第五项表示尽量选择谓语被问题所提及的三元组。
实验
数据集
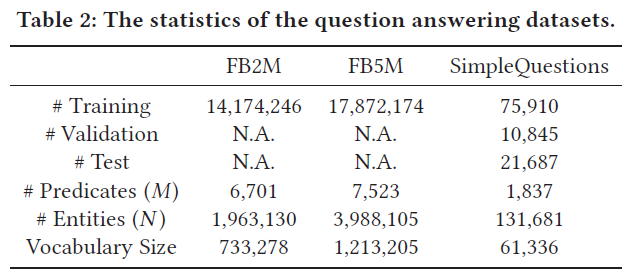
FB2M和FB5M都是Freebase的子集,包含大量结构化的数据。
SimpleQuestions包含了一万多个有相关事实的简单问题,且这些事实都存在于FB2M中
感慨
我导说我这次报告不能说服他!是我真的没看懂吗😂



