向量相似度计算方法

最近在做的嵌入模型比较，需要用到比较向量相似度，在知乎上看到了一篇文章，简单搬运过来做一些笔记和代码实践。首先列举一些向量相似度计算的方法：

1. 欧式距离（Euclidean Distance）
2. 余弦相似度（Cosine Similarity）
3. 皮尔逊相关系数（Pearson）
4. 修正余弦相似度（Adjusted Cosine）
5. 汉明距离（Hamming Distance）
6. 曼哈顿距离（Manhattan Distance）
7. 切比雪夫距离（Chebyshev Distance）

欧式距离（Euclidean Distance）

定义

欧氏距离比较容易理解，就是两点之间的直线距离，二以此类推空间中的两点$a(x_1,y_1)和b(x_2,y_2)$的欧式距离可以表示为：
$$
d=\sqrt{(x_1-x_2)^{2}+(y_1-y_2)^{2}}
$$
多维空间中的两点之间欧式距离可以表示为：
$$
d=\sqrt{(x_1-x_2)^{2}+(y_1-y_2)^{2}+(z_1-z_2)^{2}+···}
$$

实现

python简单实现：

def EuclideanDistance(x, y):
    d = 0
    for a, b in zip(x, y):  # zip将两个列表打包为元组的列表
        d += (a - b) ** 2
    return d ** 0.5

使用numpy计算：

def EuclideanDistance_np(x, y):
    # np.linalg.norm 用于范数计算，默认是二范数，相当于平方和开根号
    return np.linalg.norm(np.array(x) - np.array(y))

经测试，对于同样的两组向量，两个函数的结果相同。

余弦相似度（Cosine Similarity）

定义

首先，样本数据的夹角余弦并不是真正几何意义上的夹角余弦，只不过是借了它的名字，实际是借用了它的概念变成了是代数意义上的“夹角余弦”，用来衡量样本向量间的差异。

夹角越小，余弦值越接近1，反之越接近-1。假设有两个向量$\vec x_1,\vec x_2$:
$$
\cos (\theta)=\frac{\sum_{k=1}^{n} x_{1 k} x_{2 k}}{\sqrt{\sum_{k=1}^{n} x_{1 k}^{2}} \sqrt{\sum_{k=1}^{n} x_{2 k}^{2}}}
$$

实现

用python实现该公式：

def Cosine(x, y):
    sum_xy = 0
    num_x = 0
    num_y = 0
    for a, b in zip(x, y):
        sum_xy += a * b
        num_x += a ** 2
        num_y += b ** 2
    if num_x == 0 or num_y == 0:  # 判断分母是否为零
        return None
    else:
        return sum_xy / (num_y * num_x) ** 0.5
    
V_x = [1, 5, 7, 8, 9, 4]
V_y = [1, 4, 7, 7, 9, 3]
V_z = [2, 10, 14, 16, 18, 8]
print(Cosine(V_x, V_y)) # 0.9956602816447043
print(Cosine(V_x, V_z)) # 1.0

用numpy简化计算过程，用相同的向量测试：

def Cosine_np(x, y):
    a = np.array(x)  
    b = np.array(y)
    d = np.linalg.norm(a) * np.linalg.norm(b) 
    return np.dot(a,b) / d 


V_x = [1, 5, 7, 8, 9, 4]
V_y = [1, 4, 7, 7, 9, 3]
V_z = [2, 10, 14, 16, 18, 8]
print(Cosine_np(V_x, V_y))  # 0.9956602816447043
print(Cosine_np(V_x, V_z))  # 1.0000000000000002

欧式距离和余弦相似度的差异

来看输出结果的对比

V_x = [1, 5, 7, 8, 9, 4]
V_y = [1, 4, 7, 7, 9, 3]
V_z = [2, 10, 14, 16, 18, 8]
print(Cosine_np(V_x, V_y))  # 0.9956602816447043
print(Cosine_np(V_x, V_z))  # 1.0000000000000002
print(EuclideanDistance_np(V_x, V_y))  # 1.7320508075688772
print(EuclideanDistance_np(V_x, V_z))  # 15.362291495737216

从中可以看出

• $\vec x,\vec z$同向，他们的余弦距离为1，说明这两个向量方向一致，但是两者的欧式距离相差甚远，说明两者数值相差较大。
• 余弦相似度用来衡量两个向量之间的变化趋势，而欧式距离可以比较两个向量的数值差异

皮尔逊相关系数（Pearson Correlation Coefficient）

定义

其公式如下：
$$
\operatorname{sim}\left(x_{1}, x_{2}\right)=\frac{\sum_{k=1}^{n}\left(x_{1 k}-\overline{x_{1}}\right)\left(x_{2 k}-\overline{x_{2}}\right)}{\sqrt{\sum_{k=1}^{n}\left(x_{1 k}-\overline{x_{1}}\right)^{2}} \sqrt{\sum_{k=1}^{n}\left(x_{2 k}-\overline{x_{2}}\right)^{2}}}
$$
$\overline x$表示均值

余弦相似度会受到向量的平移影响，为了实现平移不变性，在余弦相似度的基础上，每个向量减去这个向量均值组成的向量，也就是皮尔逊相关系数。

实现

python

def Pearson(x,y):
    sum_xy = 0
    num_x = 0
    num_y = 0
    avr_x = sum(x) / len(x) # 求平均值
    avr_y = sum(y) / len(y)
    for a, b in zip(x, y):
        sum_xy += (a-avr_x) * (b-avr_y)
        num_x += (a-avr_x) ** 2
        num_y += (b-avr_y) ** 2
    if num_x == 0 or num_y == 0:  # 判断分母是否为零
        return None
    else:
        return sum_xy / (num_y * num_x) ** 0.5
    
#0.9831290611762872
#1.0

引入numpy：

def Pearson_np(x, y):
    a = np.array(x)
    b = np.array(y)
    # .corrcoef()是numpy中内置的计算皮尔逊相关系数的方法，同时需要进行归一化处理
    return 0.5 + 0.5 * (np.corrcoef(x, y, rowvar=0)[0][1])

当然也可以不使用该方法计算相似度，这里不多解释。

余弦相似度于皮尔逊相关系数的比较

V_x = [1, 5, 7, 8, 9, 4]
V_y = [1, 5, 7, 8, 9, 4]
V_z = [1, 5, 0, 8, 9, 4]
print(Cosine_np(V_x, V_y))  # 1.0
print(Cosine_np(V_x, V_z))  # 0.9450766454656805
print(Pearson_np(V_x, V_y))  # 1.0
print(Pearson_np(V_x, V_z))  # 0.819092959946616

从这个结果不容易理解皮尔逊相似系数。关于如何解释Pearson，我觉得这个回答写的比较好

他解释了为什么要中心化

中心化的意思是说, 对每个向量, 我先计算所有元素的平均值avg, 然后向量中每个维度的值都减去这个avg, 得到的这个向量叫做被中心化的向量. 机器学习, 数据挖掘要计算向量余弦相似度的时候, 由于向量经常在某个维度上有数据的缺失, 预处理阶段都要对所有维度的数值进行中心化处理.

修正余弦相似度（Adjusted Cosine Similarity）

定义

正如前文所说，余弦相似度对数值并不敏感，这种不敏感会使数值出现误差，因此我们要对其进行修正。

🌰：假设A用户为两部电影打分（1，2）B用户打分（9，10），这两个分数的余弦相似度是0.96，但是很显然，A并没有B那么喜欢第二部电影，这就产生了误差。

如何避免这种误差？答案是再引入去中心化的方法。其公式可以写成：
$$
\operatorname{adjcos
}\left(x_{1}, x_{2}\right)=\frac{\sum_{k=1}^{n}\left(x_{1 k}-\overline{x_{11}+x_{21}}\right)\left(x_{2 k}-\overline{x_{21}+x_{11}}\right)}{\sqrt{\sum_{k=1}^{n}\left(x_{1 k}-\overline{x_{11}+x_{21}}\right)^{2}} \sqrt{\sum_{k=1}^{n}\left(x_{2 k}-\overline{x_{21}+x_{11}}\right)^{2}}}
$$
仔细观察，他和公式（4）差别在哪里？每一项都减去了向量中第一项的平均值。

实现

尝试用python实现：

def AdjCosine(x, y):
    sum_xy = 0
    num_x = 0
    num_y = 0
    for a, b in zip(x, y):
        avr = (x[0] + y[0]) / 2
        sum_xy += (a - avr) * (b - avr)
        num_x += (a - avr) ** 2
        num_y += (b - avr) ** 2
    if num_x == 0 or num_y == 0:  # 判断分母是否为零
        return None
    else:
        return 0.5 + 0.5 * (sum_xy / ((num_y * num_x) ** 0.5))

使用numpy简化：

def AdjCosine_np(x, y):
    a = np.array(x)
    b = np.array(y)
    avr = (x[0] + y[0]) / 2
    d = np.linalg.norm(a-avr) * np.linalg.norm(b-avr)
    return 0.5 + 0.5 * (np.dot(a-avr, b-avr) / d)

于余弦相似度进行对比：

V_x = [1, 2, 3]
V_y = [2, 4, 6]
V_z = [3, 4, 5]
print(AdjCosine_np(V_x, V_y))  # 0.951797128930044
print(AdjCosine_np(V_x, V_z))  # 0.6889822365046137
print(Cosine_np(V_x, V_y))  # 1.0
print(Cosine_np(V_x, V_z))  # 0.9913538149119954

可以看到两者的差别还是挺大的，说明数值的确产生了比较大的影响。

❓：思考一下，如果向量中的第0个元素相同，要怎么办呢？尝试一下：

V_x = [1, 2, 3]
V_y = [1, 4, 6]
print(AdjCosine_np(V_x, V_y))  # 0.9985272427507907

果然，结果显示两个向量非常相似。要解决这个问题，我们可以参考Pearson的处理方法，用平均数构造修正函数。

def AdjCosine_np_2(x, y):
    a = np.array(x)
    b = np.array(y)
    avr = np.mean(np.append(a, b, axis=0))  # 合并矩阵并求矩阵的平均值
    d = np.linalg.norm(a - avr) * np.linalg.norm(b - avr)
    return 0.5 + 0.5 * (np.dot(a - avr, b - avr) / d)


V_x = [1, 2, 3]
V_y = [1, 4, 6]
V_z = [2, 4, 6]
print(AdjCosine_np(V_x, V_y))  # 0.9985272427507907
print(AdjCosine_np_2(V_x, V_y))  # 0.6879115070007071
print(AdjCosine_np(V_x, V_z))  # 0.951797128930044
print(AdjCosine_np_2(V_x, V_z))  # 0.5674199862463242

由结果可见，数值引起的差别被放大了，但同时也保留了余弦相似度的反映变化趋势的特征。

汉明距离（Hamming distance）

最好理解的一个：字符串之间对应位不同的数量，比如“110”和“111”的汉明距离为1，可以用在信号处理上，如果是在向量对比上效率就显得有点低了。

曼哈顿距离（Manhattan Distance）

定义

原文作者在这里提到了刘昊然原来他在唐探里提到过曼哈顿计量法。

那曼哈顿距离又是什么呢，可以看这张图：

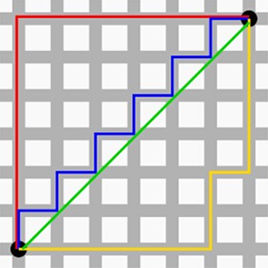
想象一下你是一个出租车司机，在曼哈顿街头，如果你想从A到B点，理论上最短距离应是直线距离，而实际上你不可能穿过一栋栋房屋直接到达B。曼哈顿距离表示的是你实际驾驶出租车从A到B的距离，该距离等于两个点在标准坐标系上的绝对轴距总和。用公式表示即

$$ \mathrm{d}_{12}=\sum_{k=1}^{n}\left|\mathrm{x}_{1 k}-x_{2 k}\right| $$

实现

def Manhattan(x, y):
    d = 0
    for a, b in zip(x, y):
        d += a - b
    return abs(d)  # 取绝对值


V_x = [1, 2, 3]
V_y = [1, 4, 6]
V_z = [2, 4, 6]
print(Manhattan(V_x, V_y))  # 5
print(Manhattan(V_x, V_z))  # 6

切比雪夫距离（Chebyshev Distance）

定义

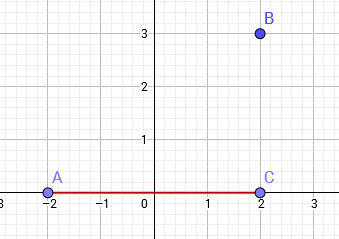
我们可以通过观察这个国际象棋棋盘来理解切比雪夫距离，国王走到棋盘上任意一点的步数，只和坐标差值中较大者有关。

更科学地定义为

切比雪夫距离：设平面空间内存在两点，它们的坐标为$(x_1,y_1)，(x_2,y_2)$ 则$is=max(|x_1−x_2|,|y_1−y_2|) $。即两点横纵坐标差的最大值 。$dis=max(AC,BC)=AC=4$。两个n维向量$(x_{11},x_{12},…,x_{1n})$与 $b(x_{21},x_{22},…,x_{2n})$间的切比雪夫距离：$d_{a b}=\max \left(\left|x_{1 i}-x_{2 i}\right|\right)$

实现

def Chebyshev(x, y):
    d = np.array(x) - np.array(y)
    return np.max(np.maximum(d, -d))  # np.maximum(a, -a)这一步相当于在取绝对值

V_x = [1, 2, 3]
V_y = [1, 4, 6]
V_z = [2, 4, -7]
print(Chebyshev(V_x, V_y))  # 3
print(Chebyshev(V_x, V_z))  # 10

总结

当然还有别的诸多距离，如闵可夫斯基距离，标准欧式距离。但是考虑到后续工作可能主要放在向量相似度的比较上，考虑使用余弦相似度相关的计算公式更合理。

以上。