原论文:graph2vec: Learning Distributed Representations of Graphs
来源:MLG 2017 - 13th International Workshop on Mining and Learning with Graphs (MLG 2017)
问题
现如今的很多研究集中在如何表示图谱中子结构的分布式表示,如节点、子图等。但是在对图的分类和聚类这些知识图谱的分析任务中,如果采用现有的手段,我们就需要得到整个图谱的表示。因此在处理这些分析任务时,图核(Graph Kernel)方法更加有效。
Graph Kernel 方法将机器学习中的核方法(Kernel Methods)拓展到了图结构数据上,是一类计算图与图之间相似度的方法。再利用图核方法比较两个图的相似度时,需要将两个图用一定方法(如最小路径,随机游走,小图等)分解成更小的子结构,再通过定义一个核函数来的到两个图的相似度(如计算两个图中相似的子结构个数)
为什么是Graph Kernels而不是用Graph Embedding?
因为后者将结构化数据降维到向量空间时,损失了大量结构化信息。而前者直接面向图结构的数据,保留了核函数高效计算的优点,又包含了结构化的信息。
文章提出,这种方式有两种存在的问题:
不能得到显式的图嵌入,不利于计算和学习。
“人为”定义的特征(路径,步伐)不具有概括性。
这些“人为”的特征应用在大型数据集上时,会产生高维的,稀疏的,不光滑的表示。
解决手段
为了解决上述的问题,文章提出了将word2vec中的Skipgram模型引入到了图谱中。在word2vec中,Skipgram的核心思想是出现在相似上下文中的单词往往具有相似的含义,因此应具有相似的矢量表示。
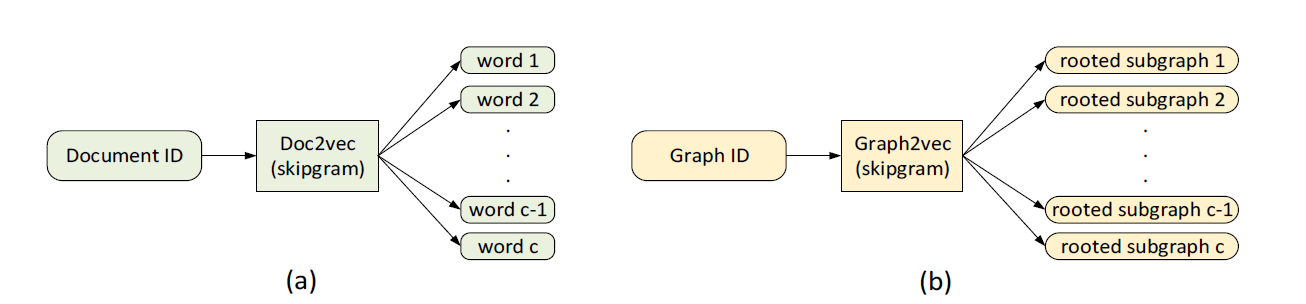
之前讲过的Doc2vec的也实在此基础上提出的。
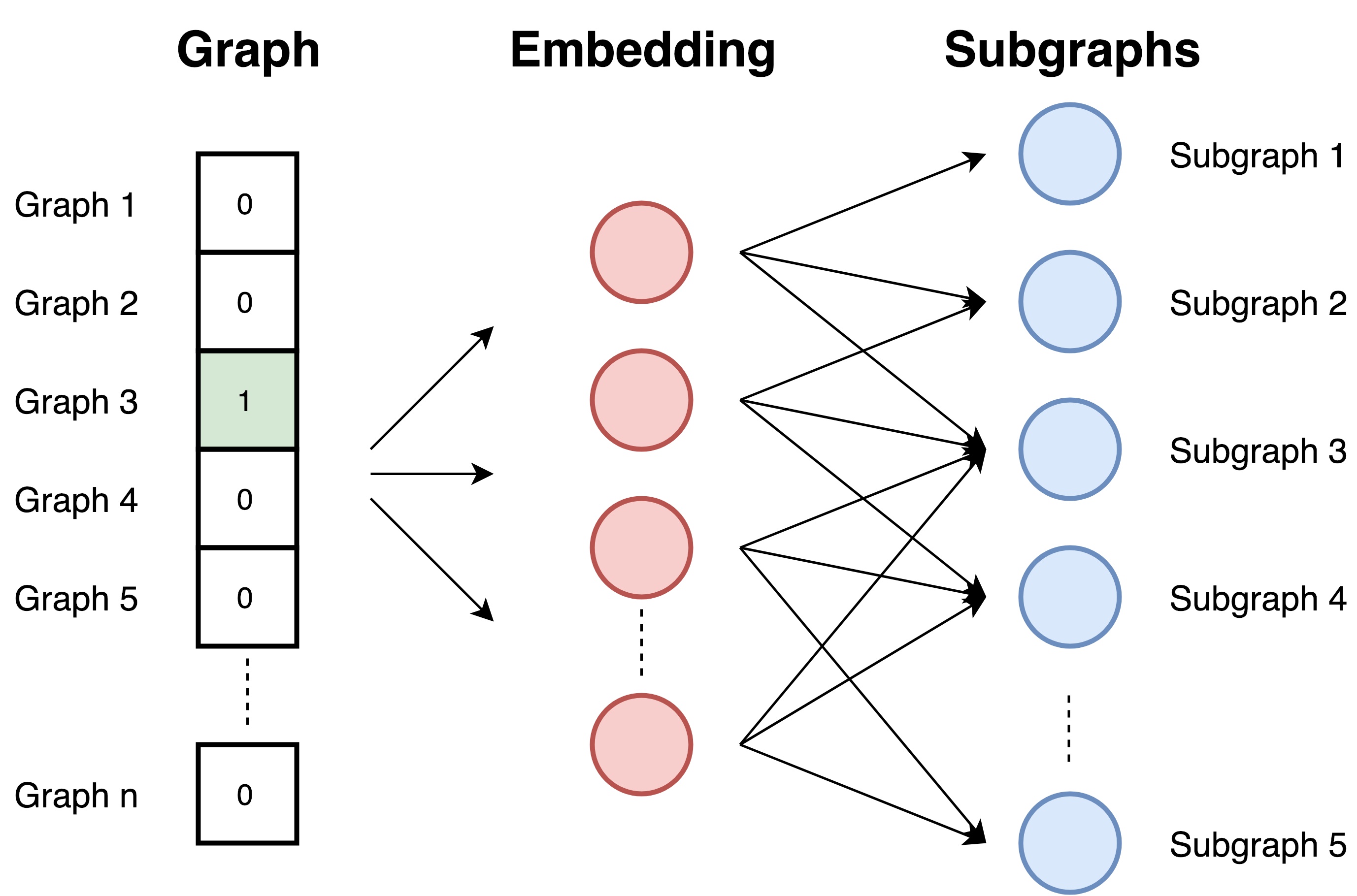
根据文章中graph2vec的思想,我们可以把一个图谱看作是一个文件(document),把图谱中的所有节点(node)周围的有根子图(rooted subgraph)看作是词(words)。换句话说,有根子图构成图谱的方式和词构成句子或段落的方式相同。具体形式如下:
为什么选用有根子图(rooted subgraph)
节点、步长和路径同样能够组成完整的图谱,那为什么要选择有根子图呢?文章给出了两个理由:
- 与节点相比,子图是一种更有序的结构;
- 与步长和路径相比,有根子图能够更好的捕获图谱中的非线性特征。因其具有图核的特性。(作者引用了一些实验结果来证明核方法能够更好的捕捉非线性特征)
算法
首先,graph2vec是一种无监督的算法,设计思路参考了doc2vec,因此再熟悉grap2vec之前,我们先复习一下doc2vec。
doc2vec
给定一个属于文档$d_i$的词$w_j$,我们要使下列预测结果R尽可能地大:
$$
R(d_i)=\sum_{j=1}^{l_{i}} \log \operatorname{Pr}\left(w_{j} \mid d_{i}\right)
$$
式中的可能性$\operatorname{Pr}\left(w_{j} \mid d\right)$,即某个段落中出现$w_j$的可能性,能够定义为:
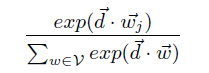
我们可以使用负采样的方法有效的训练R。
graph2vec
其主要算法流程如下:

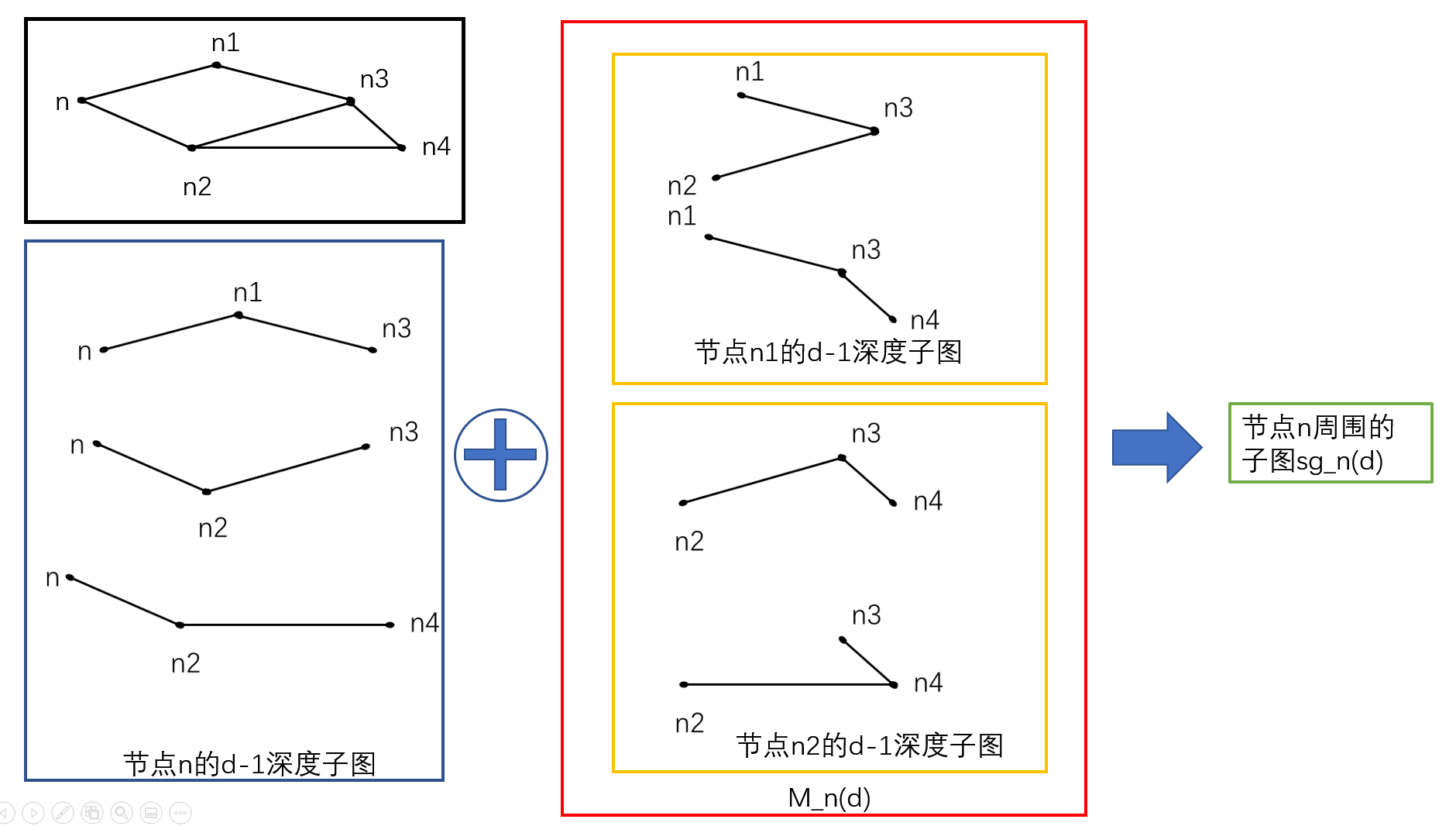
如何提取有根子图?
上面算法中的第8行用到了一个提取子图的函数GetWLSubgraph(n,Gi,d),下面来看看这个函数具体是怎么样的

文章中对这个函数给出了比较详细的解释,但是不够直观,所以我画了一个简单的例子。
如何进行负采样?
我们很容易能够看出来,算法一中的学习过程是非常昂贵的,因为整个子图词汇表会非常大。因此文章中采用了负采样的方法提高效率。即在训练图$G_i$时,引入不属于$G_i$的子图集$c={sg_1,sg_2,…}$,当然$c \in SG_{vocab}$。
如何进行优化?
使用随机梯度下降算法(SGD)来优化算法一9、10两行的参数;
使用方向传播算法来估算导数;
学习率$\alpha$按照经验调整。
总结