读论文——On2Vec:基于嵌入的本体群体关系预测
原标题:On2Vec: Embedding-based Relation Prediction for Ontology Population 来源 代码
研究背景
目标领域
本体填充(Ontology population),指将原始信息(可以是非结构化、半结构化或者结构化的数据)转换为本体实例的过程。
问题
现有的研究已经能将基于翻译的知识嵌入模式应用到实例层级的图谱中,实现较好的填充效果。相比于实例图谱,本体视图中的关系事实包含了更多复杂的语义关系,包括可传递性,对称性和层次关系。这种关系对于现有的嵌入模式来说过于复杂,且直接应用不可行。在TransE中我们用能量方程$S_{r}(\mathbf{s}, \mathbf{t})$去衡量一个三元组的可信度,函数值越小,代表描述就越准确。
$$
S_{r}(\mathbf{s}, \mathbf{t})=|\mathbf{s}+\mathbf{r}-\mathbf{t}|
$$
文章提出这种能量方程会导致如图所示的问题:

Case1:$\boldsymbol {A,B,C}$是三个概念$A,B,C$的嵌入,假设
$$
\boldsymbol {A+r\approx B,B+r\approx C}
$$
即$r$是一种具有传递性的关系,按照传递性的原则应当有:
$$
\boldsymbol {A+r\approx C}
$$
然而事实上:
$$
\boldsymbol {A + r\ne C}
$$
这个结论很容易就能从图中观察出来。Case2:$\boldsymbol {E,F}$是两个概念$E,F$的嵌入,假设:
$$
\boldsymbol {E+r\approx F}
$$
且$r$为对称性关系,则应有:$$
\boldsymbol {F+r\approx E}
$$然而事实上:
$$
\boldsymbol {F+r\ne E}
$$
这是因为向量$\boldsymbol r \ne 0$。
改进
由两个模型组件组成的On2vec,包括:
- Component-specific Model (组件特定模型)将概念和关系编码嵌入低维空间,且不丢失相关属性;
- Hierarchy Model (层次模型)集中处理层级关系。
技术路线
符号及其含义
| 字符 | 含义 | 示例 |
|---|---|---|
| $G(C,R)$ | 一个图谱 | |
| $C$ | 一系列的概念 | |
| $R$ | 一系列语义关系 | |
| $T=(s,r,t)$ | 一个三元组 | |
| $\boldsymbol s$ | vectors of source | |
| $\boldsymbol r$ | vectors of relation | |
| $\boldsymbol t$ | vectors of target | |
| $R_{tr}$ | 传递关系 | 如isConnectedTo |
| $R_s$ | 对称关系 | 如isMarriedTo |
| $R_h$ | 层级关系 | |
| $R_r$ | 将粗概念划分为细概念的细化关系 | 如hasChild |
| $R_c$ | 将细概念划分到粗概念的强制关系 | 如isLocatedIn |
| $R_o$ | 其他关系 |
我可以用不同的数学表达式展示各种关系,如传递关系$R_{tr}$
$$
given: r \in R_{tr} \ c_1,c_2,c_3 \in G \ if:(c_1,r,c_2),(c_2,r,c_3) \in G
\ then : (c_1,r,c_3) \in G
$$
建模
Component-specific Model
原理
这个名字不知道怎么翻译合适。暂时称为特定组件模型。
文章在这里认为,关系投影函数$f_r$在投影时,就已经把复杂关系中的概念放在了有冲突的位置上。为了解决这个两个问题,CSM提出了用两个不相同的$f_r$,去区别同一概念在不同三元组中的嵌入。仔细解释一下就是,对于同一个概念,在不同三元组中的组分会不同,因此在衡量一个三元组的可信度时,需要对该三元组中概念的嵌入做一定的调整才能解决这些冲突。据此文章提出了一种新的衡量可信度方程$S_{d}(T)$
$$
S_{d}(T)=| f_{1, r}(\mathbf{s})+\mathbf{r}-f_{2, r}(\mathbf{t}) \mid
$$
式中的$f_{1,r}(x),f_{2,r}(x)$是作用于头尾概念的不同组分投影函数,后文提到了这两个函数实际就是两个$k \times k $的矩阵,这两个矩阵的形式由概念在不同三元组中的组分决定。
The forms of $f_{1,r}$and $f_{2,r}$ are decided particularly by the techniques to differentiate the concept encoding under different contexts of relations.
文章还提到$S_{d}$在消除冲突的同时,还能用来实现挖掘本体中隐藏的关系。现在我们在处理Case 1时,就能把在不同三元组中的$B$放在不同的位置。对于Case 2 ,可以让$E,F$互换位置。
优化
CSM的目标是最小化能量函数,也就是增加所有三元组的可信度。和别的模型选择实体做负面样本不一样的是,CSM选择关系来做负面的样本,由此提出loss:
$$
\begin{aligned}
S_{\mathrm{CSM}}(G)=& \sum_{(s, r, t) \in G}\left[\left|f_{1, r}(\mathbf{s})+\mathbf{r}-f_{2, r}(\mathbf{t})\right|\right.\left.-\left|f_{1, r}(\mathbf{s})+\mathbf{r}^{\prime}-f_{2, r}(\mathbf{t})\right|+\gamma_{1}\right]_{+}
\end{aligned}
$$
式中的$r’$是一个并不能连接$s$和$t$的随机选取的关系,$\gamma_{1}$是一个正矩阵。学习目的是为了得到更小的$S_{CSM}$
Hierarchy Model
原理
对于层次关系,这篇文章提到了我读的另一篇论文中对层级关系的处理方法,就是让他们在向量空间上尽量聚集。如图

文章提出较为精细的概念,比如”person”,可以参与多个关系事实,这就导致了在嵌入时一个关系事实容易受到其他关系事实的影响,降低了三元组的可信度。HM要做的是将每一个精细概念的嵌入更加紧密的融合在一起。为了做到这一点,文章提出了一种精炼的操作,如图:

这一步骤是为了让所有直接相关的概念聚集,形成一个个群体。
举例说明:
设$(c_1,isA,c_2),(c_2,isA,c_3),(c_4,isA,c_3),(c_5,isA,c_3) \in G$
则有$\sigma(c_3,isA) = [c_2,c_4,c_5]$
虽然$(c_1,isA,c_2),(c_2,isA,c_3)$得到$(c_1,isA,c_3)$,但是这里认为$c_1$并不与$c_3$直接相关,故$c_1 \notin\sigma(c_3,isA)$
这样做使得群体的数量大大增加,群体之间的联系减少,减少了关系事实之间的干扰。同时也要考虑,在某一群体中处于中心的概念嵌入,在另一群体中将处于边缘,所以也需要对其嵌入做适当调整。
据此列出能量方程:
$$
\begin{aligned}
S_{h m}(G) &=\sum_{r \in R_{r}} \sum_{s \in C} \sum_{t \in \sigma(s, r)} \omega\left(f_{1, r}(\mathbf{s})+\mathbf{r}, f_{2, r}(\mathbf{t})\right) \
&+\sum_{r \in R_{c}} \sum_{t \in C} \sum_{s \in \sigma(t, r)} \omega\left(f_{2, r}(\mathbf{t})-\mathbf{r}, f_{1, r}(\mathbf{s})\right)
\end{aligned}
$$
$f_{1,r}和f_{2,r}$就是上一节写到的调整函数。$\omega (x)$是用来计算两个向量的相似度的单调递增的函数,算法中直接计算两个向量的余弦距离,余弦距离越小,余弦相似度越高。第一行计算的是所有直接细化关系的三元组的偏差,第二行计算的是所有直接强制关系的三元组的偏差,相加得到整个图谱的偏差。
优化
$$
\begin{aligned}
S_{\mathrm{HM}}(G) &=\sum_{r \in R_{r}} \sum_{s \in C} \sum_{t \in \sigma(s, r) \wedge \ t^{\prime} \notin \sigma(s, r)} S_{h r} \
&+\sum_{r \in R_{c}} \sum_{t \in C} \sum_{s \in \sigma(t, r) \wedge \ s^{\prime} \notin \sigma(t, r)} S_{h c}
\end{aligned}
$$
$s’$和$t’$在这里做负面样本,其中
$$
S_{h r}=\left[\omega\left(f_{1, r}(\mathbf{s})+\mathbf{r}, f_{2, r}(\mathbf{t})\right)-\omega\left(f_{1, r}(\mathbf{s})+\mathbf{r}, f_{2, r}\left(\mathbf{t}^{\prime}\right)\right)+\gamma_{2}\right]_{+}
$$
$$
S_{h c}=\left[\omega\left(f_{2, r}(\mathbf{t})-\mathbf{r}, f_{1, r}(\mathbf{s})\right)-\omega\left(f_{2, r}(\mathbf{t})-\mathbf{r}, f_{1, r}\left(\mathbf{s}^{\prime}\right)\right)+\gamma_{2}\right]_{+}
$$
学习流程
学习的目标是联合损失最小,联合损失的表达式如下
$$
J(\theta)=S_{\mathrm{CSM}}+\alpha_{1} S_{\mathrm{HM}}+\alpha_{2} S_{\mathrm{N}}
$$
- $\theta$ 是包括嵌入向量和投影矩阵的一系列的参数的集合
- $\alpha_{1} S_{\mathrm{HM}}$中的$\alpha_1$用来调整两个模型的权重
- $\alpha_1S_N$中的$\alpha_1$是一个大于零小于等一的数,$S_N$用来对嵌入和投影施加约束,防止出现向量趋向于无限大的情况。其形式如下

最后给出了具体算法流程如图

数据集
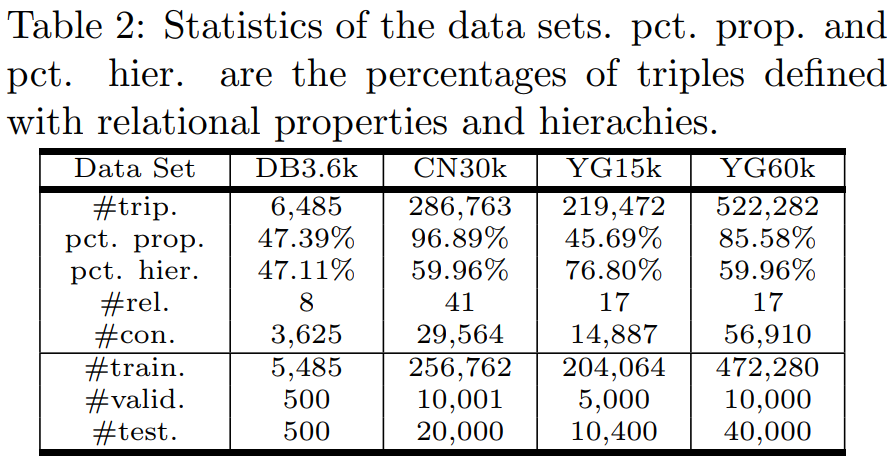
在实验中,这个模型被用来做关系预测和关系识别。关系预测准确率在90%左右,关系识别的准确率波动较大,最高有98%,最低73%
写在最后
这篇论文看的我蛮痛苦的,因为里面好多用词都不是那么精准,而且也没有合适的图例表达算法逻辑,和之前发出来那篇差了好多,许多地方并不能说服我,有时间再看看他的源码吧。果然好论文一定是容易读的论文!



