1.1__算法的基本概念
算法的重要属性——正确和高效
1.2__算法举例
局部高点
定义:存在列表$A$,若$A[i-1] \leq A[i] \geq A[i+1]$,则称$A[i]$为局部高点。不是所有序列都有局部高点,这里限制边界条件$A[-1] = A[n]= -\infty$。
简单算法:
找出数列中任意一个局部高点
逐个索引,比较前后元素之间的大小
- 最好的情况:第一个元素就是局部高点
1次 - 最坏的情况:最后一个元素才是局部高点
n次
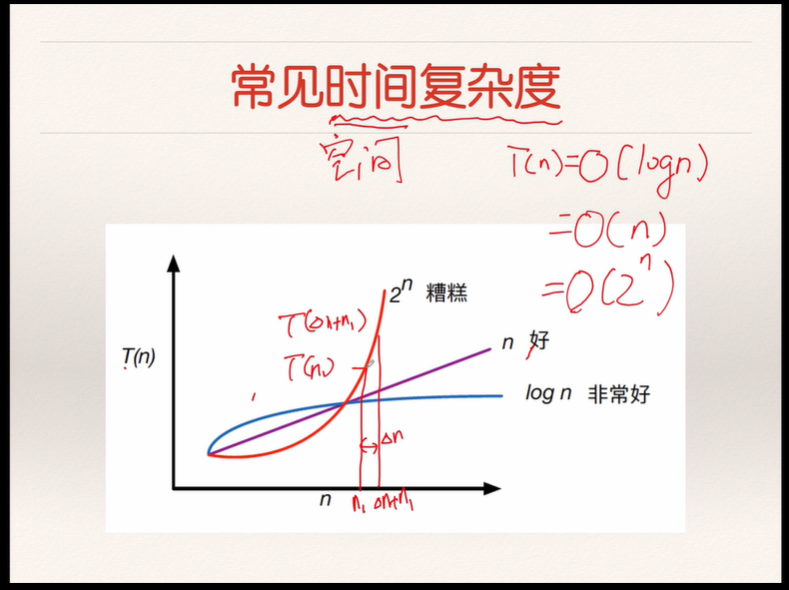
算法分析应考虑最坏的情况,实际分析中应尽量忽略数据的分布
所以简单算法的效率事$O(n)$,函数是一个单调递增的线性函数
更高效的算法:
考虑每次查找都缩小查找的范围
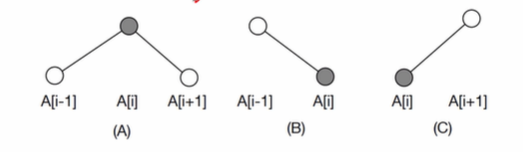
从中间的元素开始查找,可以在一次比较后,缩小一半的搜索范围(二分法)
算法的效率为$O(log_2n)$



