标题:Structural Similarity Search for Formulas Using Leaf-Root Paths in Operator Subtrees
作者:Wei Zhong and Richard Zanibbi
期刊:Advances in Information Retrieval
看这篇文章之前,提出了两个问题:
- 如何把公式转化为操作树?
- 与之前接触过的树相似度算法有何不同?
关键问题
以何种形式表达数学公式?

数学公式的相似性如何衡量?
- 结构的相似性
- common subexpression:是否都存在相同的子表达式
- operator commutativity:交换律
- operator associativity:结合律
- 符号的相似性
- $(1+1/n)^n$与$(1+1/x)^x$ 虽然符号不同,但是$n$和$x$都表示未知数,语义相同,所以这两个是相同的公式;
- $e=mc^2$与$y=ax^2$ 在考虑物理意义的条件下,是两个不同的公式;
- 语义的相似性
- 等效的公式$1/x$和$x^{-1}$,就和苹果与apple一样
- 结构的相似性
方法
这部分描述了如何定量的衡量两个公式之间的相似度
将$\LaTeX$转化为操作树(OPT)。将比较公式相似度的问题转化为比较
- 比较树的结构
- 比较节点的名称
下面的定义描述了如何度量两个树之间的相似度。
定义1 公共子树
公式树$Tq$和$T_d$,他们的公共子树包含两个部分,即这两个公式中结构一致的子树$\hat{T}_q$和$\hat{T}_d$,且子树的叶节点为公式树的叶节点。用公式可以表达为:
$$ CFS\left(T_{q}, T_{d}\right)=\left\{\hat{T}_{q}, \hat{T}_{d}: \hat{T}_{q} \preceq_{l} T_{q}, \hat{T}_{d} \preceq_{l} T_{d}, \hat{T}_{q} \cong \hat{T}_{d}, \hat{T}_{q} \subseteq T_{q}, \hat{T}_{d} \subseteq T_{d}\right\} $$其中$“\cong”$表示同构,$“\subseteq”$表示从属关系,而$“\preceq_{l}”$表示子树的叶节点为操作树的叶节点,用图片来说明
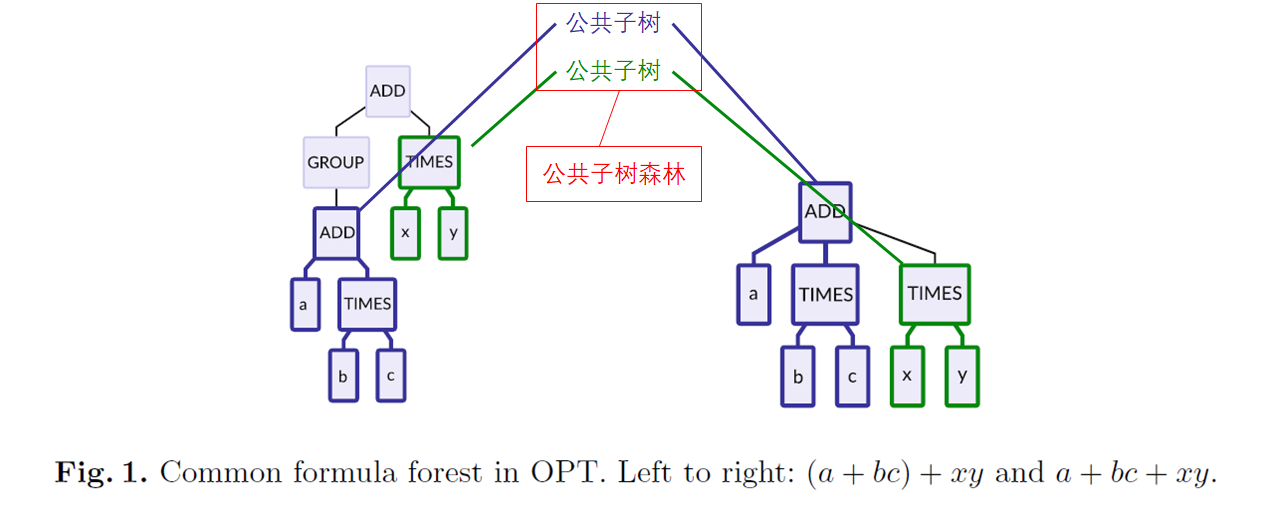
定义2 公共子树森林
公共子树森林(common formula forest)是所有不相连的公共子树的集合,一个公共子树森林可以用公式表示为:
$$ \pi=\left\{\left(\hat{T}_{q}^{1}, \hat{T}_{d}^{1}\right),\left(\hat{T}_{q}^{2}, \hat{T}_{d}^{2}\right), \ldots\left(\hat{T}_{q}^{n}, \hat{T}_{d}^{n}\right)\right\} \in \Pi\left(T_{q}, T_{d}\right)\qquad(1) $$两个表达式之间可能存在多个不同的公共子树森林,都属于$\Pi\left(T_{q}, T_{d}\right)$。
公共子树森林可以表示两个数学表达式中的相似部分,那使用这个森林去度量相似度呢?
定义3 度量相似度
$$ \Gamma_{\gamma}\left(T_{q}, T_{d}\right)=\max _{\pi \in \Pi\left(T_{q}, T_{d}\right)} \gamma(\pi)\qquad(2) $$ $$ \gamma(\pi)=\sum_{\left(\hat{T}_{q}^{i}, \hat{T}_{d}^{i}\right) \in \pi} \beta_{i} \cdot\left(\alpha \cdot \text { internals }\left(\hat{T}_{d}^{i}\right)+(1-\alpha) \cdot \operatorname{leaves}\left(\hat{T}_{d}^{i}\right)\right)\qquad(3) $$$internals \left(T\right)$: T中节点或操作符的数目
$leaves(T)$:T中叶节点/运算对象的数目
$\alpha$:大于0小于1,操作符贡献的权重
$\beta_i$:大于0,子表达式贡献的权重,子表达式的范围越广,贡献的权重越大。实际计算中,对于一些范围小的子树,该值取0
子表达式匹配
这一部分讲述了如何进行子表达式的匹配,侧重提高检索速率。
以路径为最小单元进行匹配,这样做的话相比于运算符,匹配运算对象更加容易。
这里可能是因为运算符的形式会比运算对象的形式差异更大,如$1/x$和$x^{-1}$
文中提出了一种贪心算法,在一次检索流程中,先找到运算对象最多的$\pi$,再去计算这个$\pi$当中运算符的数量,通过公式3计算本次的得分。最后比较所有检索对的分数。
贪心算法
假设1:如果$\pi^{*}=\left\{\left(\hat{T}_{q}^{1 *}, \hat{T}_{d}^{1 *}\right),\left(\hat{T}_{q}^{2 *}, \hat{T}_{d}^{2 *}\right) \ldots\left(\hat{T}_{q}^{n *}, \hat{T}_{d}^{n *}\right)\right\} \in \Pi\left(T_{q}, T_{d}\right)$ 能够使公式2在 $\alpha=0$ 且 $\beta_{1} \gg \beta_{2} \gg \ldots \gg \beta_{n}$取到最大值,那就认为在 $\alpha \neq 0$ 且 $\beta_{1} \geq \beta_{2} \geq \ldots \geq \beta_{n}$时, $\pi^{*}$ 也能让其取到最大值。
在该假设的第一个条件下,公式3的形式是
$$ \gamma(\pi)=\sum_{\left(\hat{T}_{q}^{i}, \hat{T}_{d}^{i}\right) \in \pi} \beta_{i} \cdot{leaves}\left(\hat{T}_{d}^{i}\right) $$在该假设下,范围越广、运算对象越多的公共子树得分越高,从而使得其属于的公共子树森林得分越高。
同时文章也想要一种更有效地找到相似结构的方式。
假设$P(T)$是公式树T所有叶节点到根节点的路径,$M(S_1, S_2,E)$表示使用二分图的形式表示路径集合$S_1、S_2$之间的匹配关系,$E$二分图中的边(连线),在此基础上提出假设2:
假设2:对于任意的树 $T_{q}, T_{d}$, $S_{q}= P \left(T_{q}\right), S_{d}= P \left(T_{d}\right)$如果存在完美的匹配 $M\left(S_{q}, S_{d}, E\right)$,即每一条路径都能在另一个树中找到对应的路径,那就可以认为$T_{q} \cong T_{d}$。当然这个假设并不是所有情况下都成立的,比如下图的两个公式:
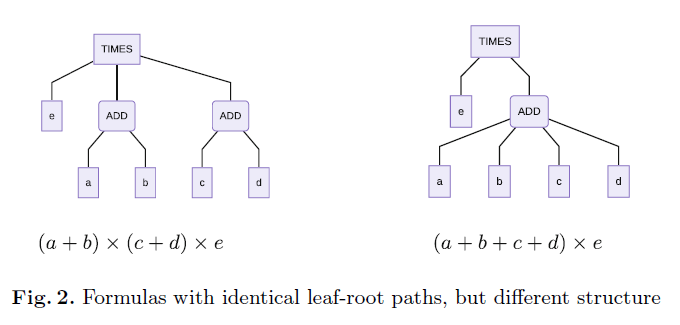
那既然存在不成立的情况,为什么还要做出这样的假设呢?作者给出的理由包括:
- 这种情况相对少见;
- 希望设计一个更具有实用意义的搜索算法(快速)。
但看这张图中的这个表达式,这种情况真的少见吗?
在这两个假设下,作者完整的描述了搜索相似公式的算法

检索
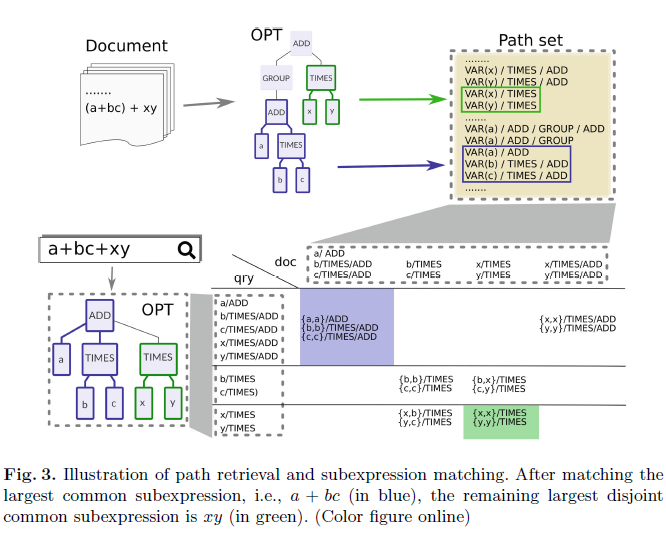
- 转化为操作树
- 操作符,操作对象的令牌化:制定100+语法规则,50+符号类型。
- 路径的生成:对于每一个操作符,都将其标记为根节点,记录所有叶节点到该节点的路径。
- 记录的数据:路径的ID,操作符号和对象的ID
总体的相似度计算公式:
$$
\frac{S_{ st } S_{ sy }}{S_{ st }+S_{ sy }}\left[(1-\theta)+\theta \frac{1}{\log \left(1+\operatorname{leaves}\left(T_{d}\right)\right)}\right], \quad \theta \in[0,1]\qquad(4)
$$
其中$S_{st}$是结构相似度的得分,计算方式:
$$
S_{ st }= \begin{cases}\frac{\Gamma_{\gamma}\left(T_{q}, T_{d}\right)}{\operatorname{leaves}\left(T_{q}\right)} & \text { if } \alpha=0 \ \frac{\Gamma_{\gamma}\left(T_{q}, T_{d}\right)}{\operatorname{leaves}\left(T_{q}\right)+\text { internals }\left(T_{q}\right)} & \text { if } \alpha \neq 0\end{cases}\qquad(5)
$$
$S_{sy}$是标准化的操作符号集的相似度,计算方式:
$$
S_{ sy }=\frac{1}{1+(1-y)^{2}}\qquad(6)
$$
其中$y \in[0,1]$,来自另一个算法Mark-and-Cross(Zhong, W., Fang, H.: A novel similarity-search method for mathematical content
in LaTeX markup and its implementation. Master’s thesis, University of Delaware)
总结与思考
这篇文章解决了哪些问题?
采用匹配叶根路径的方法,度量公式结构的相似度;使用贪心算法提高搜索的效率。
如何把公式转化为操作树?
这篇文章并没有详细描述转化为操作树的过程。查阅了这篇文章所引用的文献,对于将$\LaTeX$转化为树结构的问题,《Recognition and retrieval of mathematical expressions》这篇文章提到了,转化主要还是依靠制订一系列的语法规则。
与之前的树相似度算法有何不同?
考虑时间复杂度和搜索的效率。



