背景
标题:Image-to-Markup Generation with Coarse-to-Fine Attention
作者:Yuntian Deng, Anssi Kanervisto, Jeffrey Ling, Alexander M. Rush
来源:International Conference on Machine Learning,2017
应用背景:面向数学公式的图像识别以及标记语言生成

问题
- 在不包含文本或者视觉语法(\frac,^)信息的情况下,一个监督学习模型是否能够完成从图像生成正确的标记语言的任务;
- 如何将一个渲染的公式转化成能够描述内容和布局的标记语言(markup)?
目标
监督任务的目标是什么?
$x$ 包含了一张图片,$y$ 包含了一系列的标记语言的token $y_1,y_2,…y_T$
假设将标记语言转换成图片是一个编译过程(实际上是一个渲染的过程),即$compile(y)\approx x$(黑盒,不包含文本信息或者视觉语法),如果能够实现对 $compile$ 的反编译,那么就可以实现从图像生成标记语言的目标;
如何去检验准确性?
给定一个由 ground-truth $y$ 渲染得到的 $x$ ,系统生成一个假设的 $\hat y$,再通过一个黑盒函数编译 $compile(\hat y)= \hat
x$,评估$x$与$\hat x$之间的相似性。训练目标是生成相似的图像,而 $\hat y$ 可能与 $y$ 相似,也可能不相似。
模型
精确的识别一个从左到右写出来的公式并不难,传统的方式已经可以解决这个问题。但是当公式中存在上下的顺序,比如分数、求和符号的注释时,传统的方式精确度就不是那么高了。所以要提高识别的精度,核心问题时如何选取出公式中的特殊区域。
特征提取
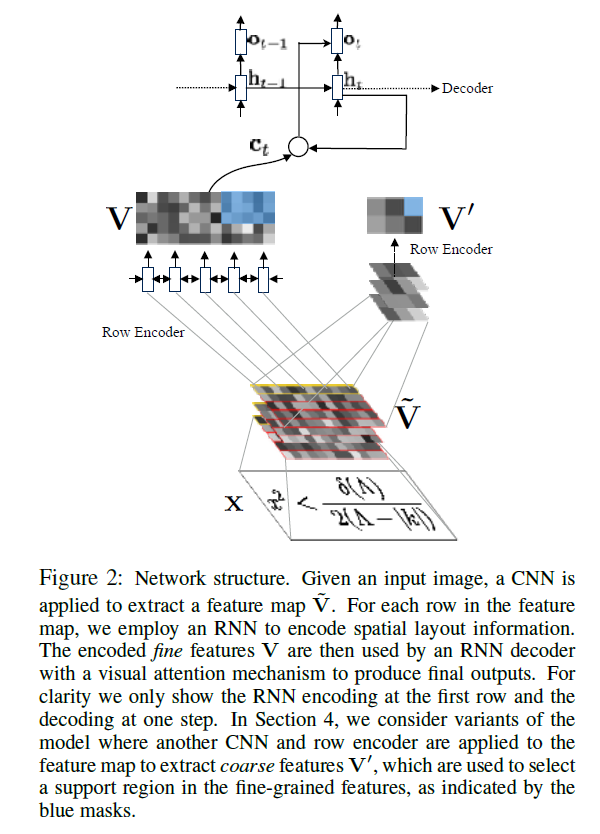
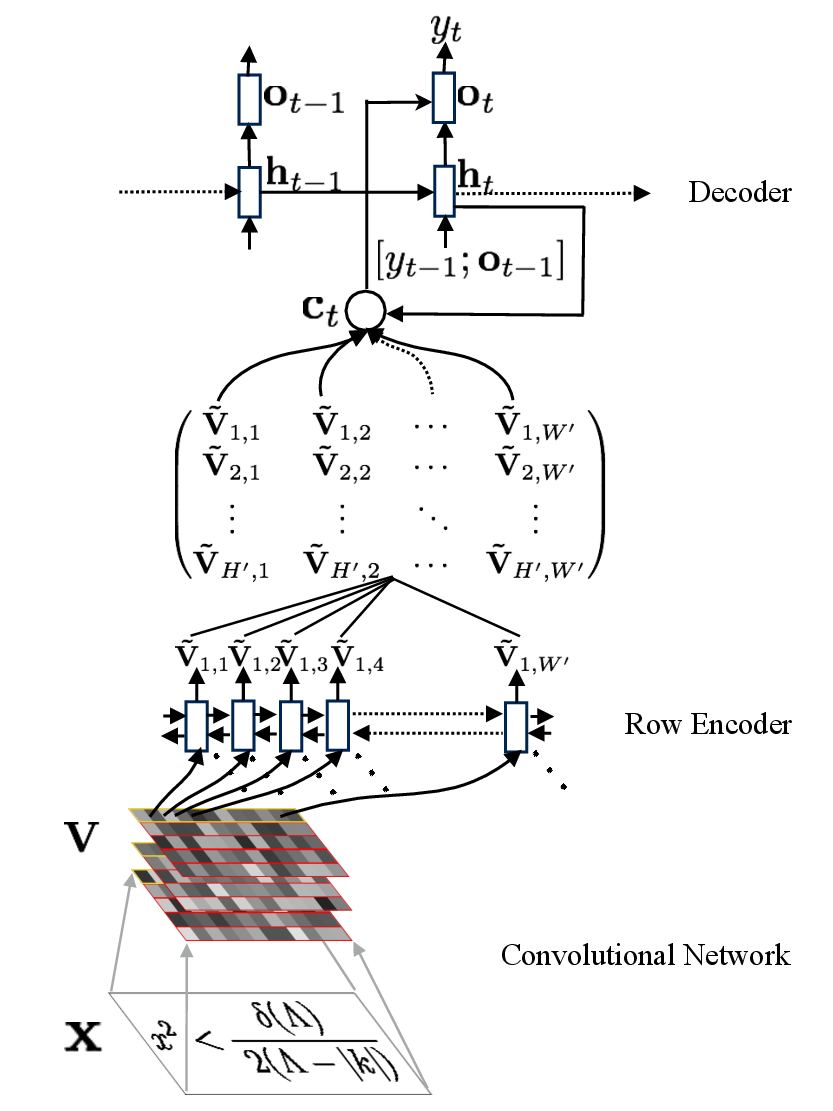
图片的视觉信息由一个多层的CNN抽取,文中提到了与如今的一些使用CNN的OCR模型不同的是,该模型没有使用全连接层,为的是保留CNN抽取特征的局部性以引入视觉注意力。CNN的输入是原始数据,输出一个特征网格$\tilde{ V }$,该网格的大小是$D \times H \times W$,其中$D$是通道数,$H$是特征图的高,$W$则是宽。
行编码器
在图像描述生成任务中,不需要对CNN提取的特征进行处理。但在OCR任务中,我们需要指导相关的位置信息。以往都使用CTC(Connectionist Temporal Classification )定位,在本文的方法中,通过对 $\tilde{ V }$ 的每一行运行RNN以生成新的特征网格$V$。新的特征单元格可以被定义为$V_{hw}=RNN(V_{h,w-1},V_{hw})$,对每一行初始化可训练的隐藏层$V_{h,0}$,将其称之为位置向量。
由此,新的特征网格既包含了位置信息又包含了序列信息。
作者补充到,实验中所有RNN都是LSTM网络。
关于什么是CTC,这篇文章做了详细的描述。CTC主要被用来处理语音识别,手写字体识别和其他一系列的序列问题。主要的作用是处理输入与输出的“对齐”问题,比如
图中的两个任务,对于一个输出,他的输入长度可能是不断变化的。但同时我们也可以从中看出,CTC处理的输入是严格按照从左到右的顺序排列的。
解码器
文中的解码器是一种条件语言模型,该模型根据解码的历史和注释来给出下一个可能的token。文中将其表示为:
$$
p\left(y_{t+1} \mid y_{1}, \ldots, y_{t}, V \right)=\operatorname{softmax}\left( W ^{\text {out }} o _{t}\right)
$$
$$
o _{t}=\tanh \left( W ^{c}\left[ h _{t} ; c _{t}\right]\right)
$$
- $W ^{\text {out }}, W ^{c}$ 是学习到的线性变换函数;
- $h _{t}= R N N \left( h _{t-1},\left[y_{t-1} ; o _{t-1}\right]\right)$ 包含了历史的解码信息;
- $c_t$ 是上下文向量,包含了来自于注释网格的上下文信息,具体怎么得到见下一节。
标记语言生成中的注意力机制
由上文可见,识别的准确率在于是否能够追踪到当前位置的下一位置,而这个信息由注意力集中的向量 $c_t$ 传达。那 $c_t$ 是如何得到的?
首先定义一个分类向量 $z_{t} \in{1, \cdots, H} \times{1, \cdots, W}$ ,用来描述模型正在关注哪个单元格 。假设注意力分布$p\left(z_{t}\right)$ 。那么上下文向量可以表示为:
$$ c _{t}=\sum_{h, w} p\left(z_{t}=(h, w)\right) V _{h w} $$那问题又被转化为:如何获取注意力分布?文章描述了三种方法:
标准注意力(Standard Attention)
该方式可以表示为:
$$ p\left(z_{t}\right)=\operatorname{softmax}\left(a\left( h _{t},\left\{ V _{h w}\right\}\right)\right) $$其中$a(·)$是一个神经网络,用来产生非归一化的注意力权重,该神经网络有许多不同的形式,文章中选择了$a_{t,h,w}=\beta^{T} \tanh \left(W_{1} h _{t}+W_{2} V _{h w}\right)$
那这样做是否可以满足要求呢?文章中提到了三个关于OCR任务中注意里分布的必要关键属性:
- 网格要足够精细,才能保证能够定位到当前符号,这就使得网格总数增加了不少;
- 在实际的应用中,注意力分布的主要作用仅仅体现在识别某个小区域内的某个符号;
- 按照上文中的公式,在每个时间步中的每个单元格上都跑一遍注意力,其解码的复杂度可以表示为 $O(T H W)$
综上三点,这种注意力机制在处理较大的图像时效率很低,或者说,投入与产出不成正比;
分层注意力(Hierarchical Attention)
策略是在图片上添加一层粒度更粗的网格,在生成标记符号时,首先根据上一步结果从粗粒度的网格中获取一个相关区域,再在这个区域内的单元中获取上下文向量。该机制下的注意力分布可以表示为:
$$
p\left(z_{t}\right)=\sum_{z_{t}^{\prime}} p\left(z_{t}^{\prime}\right) p\left(z_{t} \mid z_{t}^{\prime}\right)
$$
$p\left(z_{t}^{\prime}\right)$ 表示在粗粒度网格上的注意力分布,由标准注意力获得。
计算$p\left(z_{t}^{\prime}\right)$ 的复杂度为 $O\left(H^{\prime} W^{\prime}\right)$,计算$p\left(z_{t} \mid z_{t}^{\prime}\right)$ 的复杂度为$O\left(\frac{H}{H^{\prime}} \frac{W}{W^{\prime}}\right)$,则在这种方法下计算$p\left(z_{t}\right)$的复杂度仍有$O\left(H W\right)$
由粗到细的注意力(Coarse-to-Fine Attention)

目标是通过缩小可能的粗粒度单元格范围来实现降低时间复杂度;
强化学习
文章提出了使用强化学习来解决这个问题,以选取困难样本(hard sample)而不是考虑整个区域的方式来获取$p\left(z_{t}^{\prime}\right)$,使用以下几个参数来描述该强化学习算法,包括:
- 随机动作:选择t时刻的区域 $z_{t}’$
- 奖励: 输出的符号与正确符号之间的对数似然函数值
- 全局奖励:
- 反向传播的策略梯度:
$$
r_{t} \cdot \frac{\partial \log p\left(z_{t}^{\prime} ; \theta\right)}{\partial \theta}
$$
RNN解码器之下的奖励:
由于在解码阶段使用了RNN,所以每个当前动作 $Z_t’$ 都会对之后的奖励 $r_t,r_{t+1},…r_T$ 产生影响,文章重新定义了奖励,其形式为:
$$ \tilde{r}_{t}=\sum_{s=t}^{T} \gamma^{s} r_{s} $$其中 $\gamma$ 是一个大于0小于1的数。
实际应用中的的策略梯度:
$$ \frac{\partial L }{\partial \theta}=\left(\tilde{r}_{t}-b_{t}\right) \cdot \frac{\partial \log p\left(z_{t}^{\prime} ; \theta\right)}{\partial \theta} $$其中
$$ b_{t} \leftarrow \beta b_{t}+(1-\beta) \tilde{r}_{t} $$$b_{t}$ 为一个可变的平均奖励基线,从而降低方差,减少噪音。
时间复杂度
在该强化学习模型初选区域的基础上,注意力的时间复杂度变成了:
$$
O\left(\frac{H}{H^{\prime}} \frac{W}{W^{\prime}}+H^{\prime} W^{\prime}\right)
$$
当$H^{\prime}=\sqrt{H}, W^{\prime}=\sqrt{W}$时,时间复杂度为:
$$
O(\sqrt{H W})
$$
其他贡献
- 创建了一个包含103556个不同 $\LaTeX$ 公式及其渲染图片的数据集。
总结
- 发散性思维以及问题简化能力;
- 广泛的文献阅读、实践能力。




